PINNs - Physics Informed Neural Networks

Physics-informed neural networks (PINNs) are a revolutionary approach that integrates physical laws and governing equations directly into neural network training. By embedding domain knowledge from physics into the learning process, PINNs achieve superior accuracy, interpretability, and data efficiency compared to traditional data-driven models. This methodology enables the solution of forward and inverse problems across various physics domains, from fluid dynamics to electromagnetics, while requiring minimal training data.

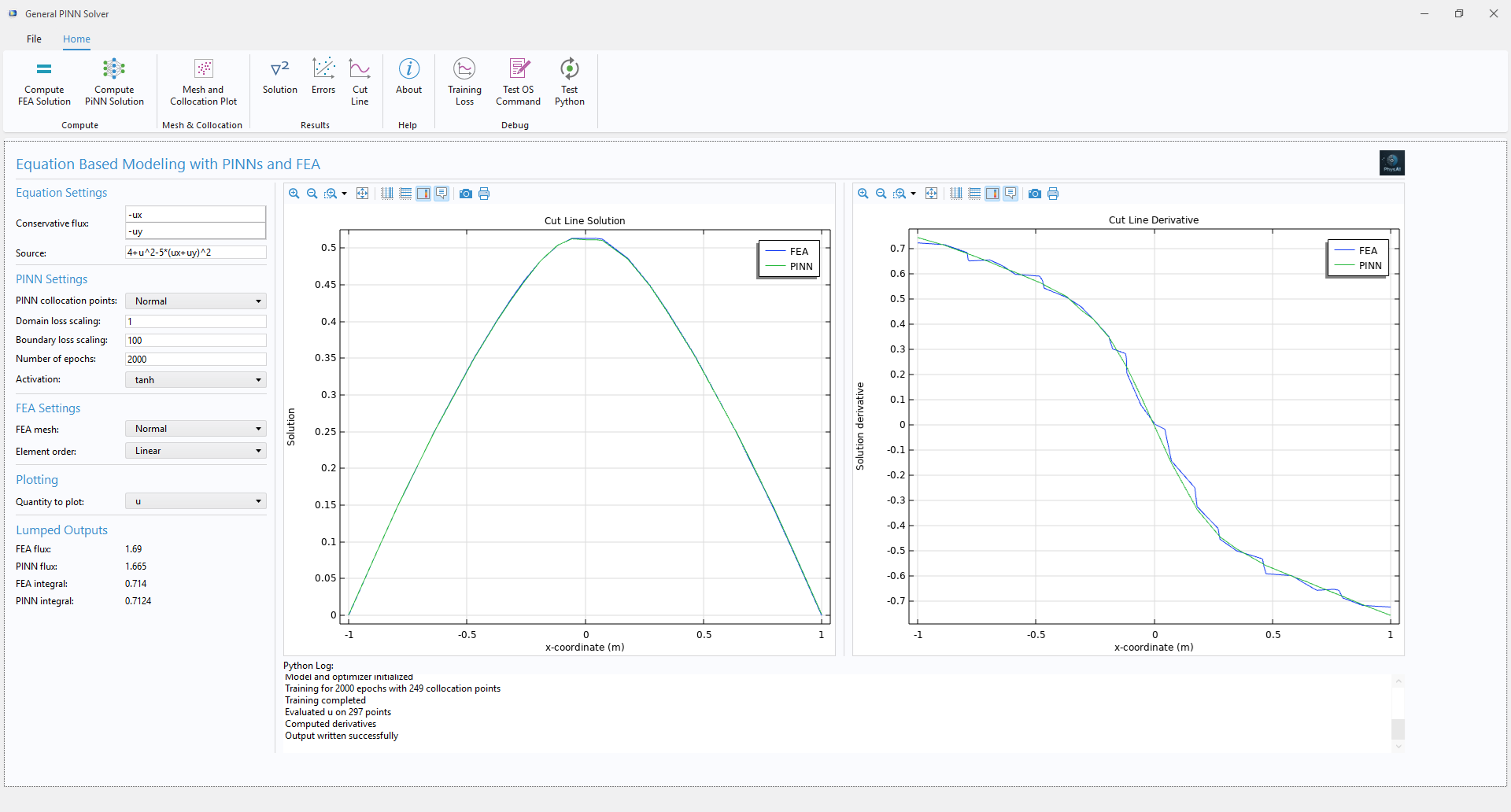
Shown below is an example of a nonlinear partial differential equation that can be specified in the App. As a test, the following problem is solved:

\[ \nabla \cdot (-\nabla u)=4+u^2-5 \left(\frac{\partial u}{\partial x} + \frac{\partial u}{\partial y} \right)^2 \]

and on boundaries a Dirichlet boundary condition is applied:

\[ u = 0 \]

Equation-based Modeling using PINNs

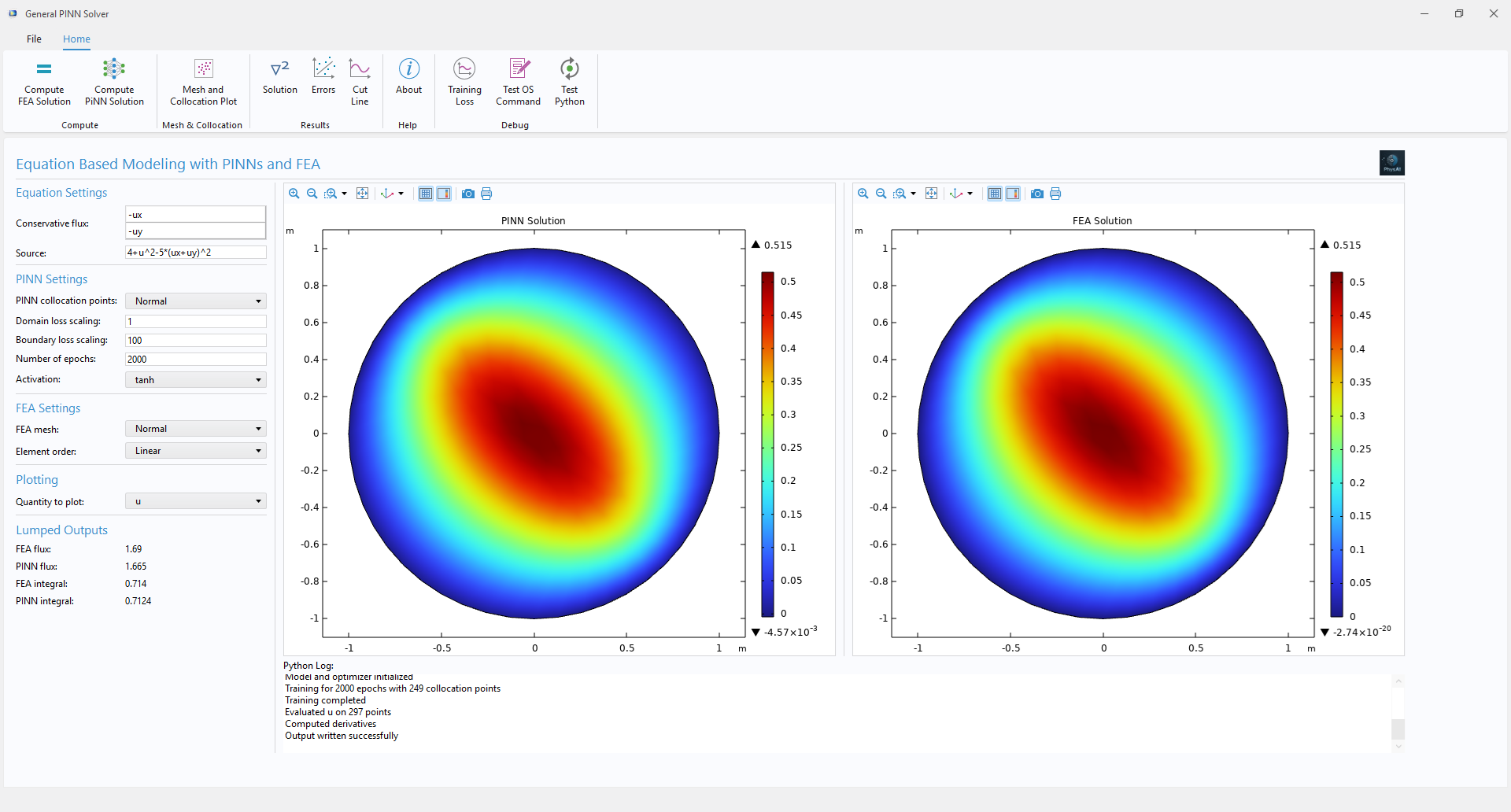
Shown below is a COMSOL app which allows you to specify an arbitrary linear or nonlinear partial differential equation, and the PINNs method is used to solve the problem. In addition, the traditional FEA method used by COMSOL is used to solve the same problem to better quantify and analyze errors.

Equation based modeling using PINNs Arbitrary linear or nonlinear partial differential equations can be specified in the GUI.

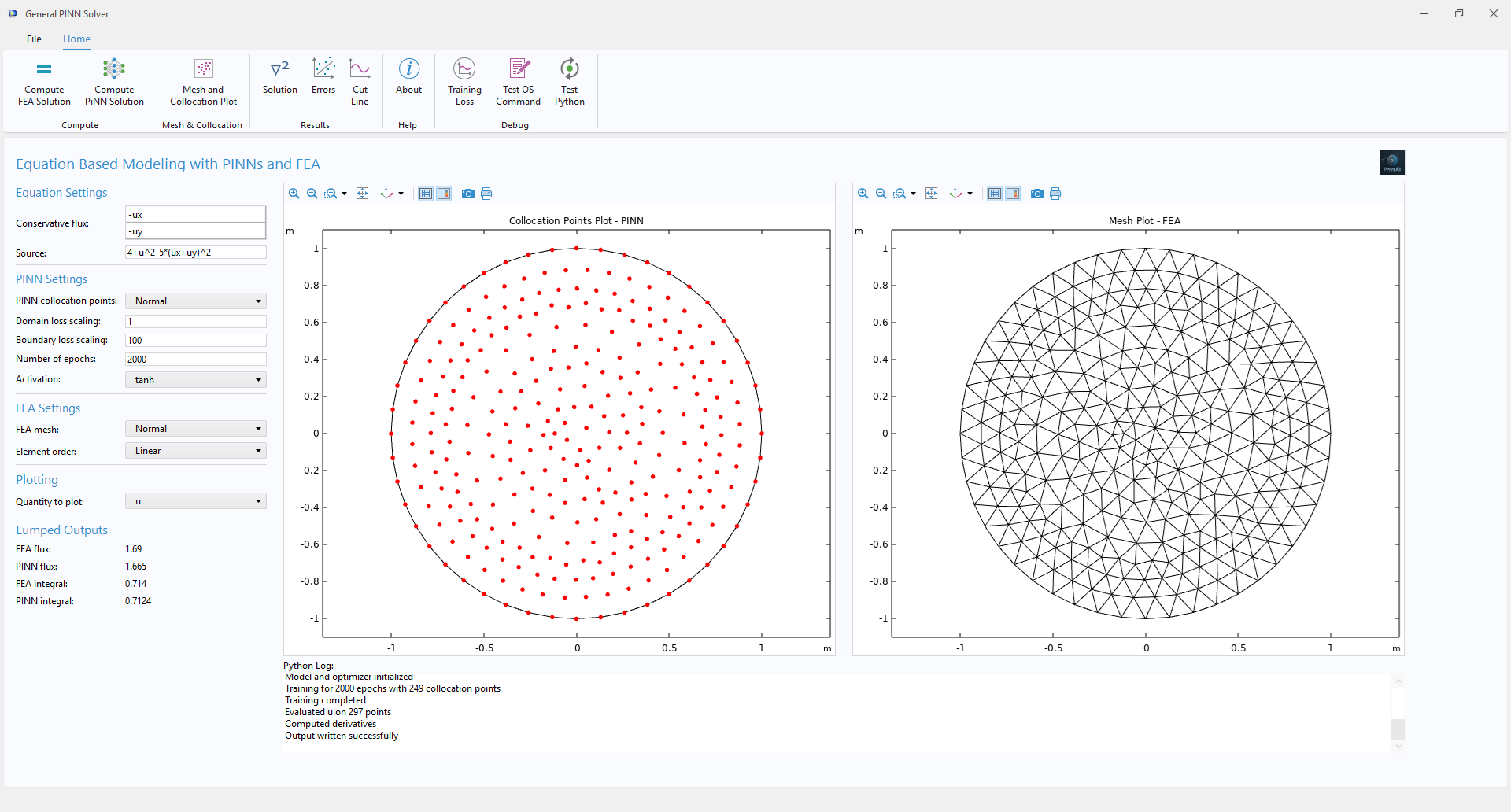
The collocation points for the PINN discretization are shown below along with the traditional mesh used by the conventional finite element method.

Collocation points and traditional FEA mesh The collocation points are shown to the left in red and the traditional FEA mesh is shown to the right in black.

A comparison of a cut line from x=-1 to 1 at y=0 is shown below for the PINN and the traditional FEA method. When linear shape functions are used for the finite element method, the derivative of the solution is not smooth and continuous like it is for the PINN.

Cut line of the solution and derivative along the x-axis at y=0 The derivative of the solution is noticeably smoother for the PINN than for the traditional FEA method.